- Spark work on a master - slave model.
- Master Machine and Slave Machines required. You can have master and slave on same machine too.
- For testing purpose you can generate the cluster on same machine , approach similar
- In each machine check if Java is installed
JAVA install/update - If you are using a new machine, ec2 it wont come preinstalled with Java.
- You can set up Java following below steps
- First update package index :
- sudo apt-get update
- check version java -version
- If Java not found → Install JRE
- sudo apt-get install default-jre
- sudo apt-get install default-jdk
- check Java-version
- This might install Java 1.6
- sudo apt-get install openjdk-7-jre
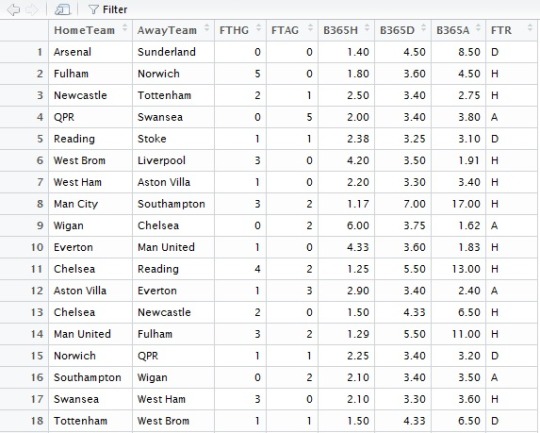
- sudo apt-get isntall openjdk-7-jdk
- Issue : Java still points to version 6.
- Follow below steps to update
- update java-alternatives -l
- sudo update-java-alternatives
s java1.7.0-openjdk-amd64 (your path to the newer)
Instance Setup - Login to Dev or EC2 instances
- If Running on Ec2 Do the following:
- Create an account, generate private and public key pairs download the keys to one of the machine. You can get those steps online on how to generate key pairs.
- Create two system variables for AWS_ACCESS_KEY and AWS_SECRET_KEY
- Go to spark directory on your local machine and run the ec2 script from ./sbin/ec2 file.
- ./spark-ec2 --key-pair=awskey --identity-file=awskey.pem --region=us-west-1 --zone=us-west-1a launch my-spark-cluster
- This will create two Large instances cluster.
SetUp Spark - Download Spark → Select Hadoop latest Version and follow the link
- For dev box : you can download using :
- wget spark link
- unzip using tar -xzf folder for spark
- Do this in all machines you want to run spark on .
- Set up env variable SPARK_HOME to point folder just before the bin directory, in normal case it will be the unzipped folder
- Save it using source ./bashrc
- Decide on which machine you want your master and slave
Master Machine - Login to Master Machine, follow below steps
- edit hosts file for master
- vi /etc/hosts
- Provide the link between IP and name
- IP Machine1
IP Machine 2
- Next few steps are changes in spark code
- slaves template is located in the conf directory.
- there is a file called slave template, same file can be used or a new file called you can create from that buy copying the content to slaves
- Paste the names of all slaves in this file
- slave 1
- slave 2
- slave 3
- Go to Spark Sbin Directory
- cd ./sbin/
- run ./sbin/start-master.sh
- This will start the master on port 8080, access it via IP address or Machine Name
- For current case go to any web browser and type : http://machinename:8080
- This was required because you need to get the spark master address. When you go to the link it will show the url at the top spark://machinename:7077
- Copy it
- Go to /conf/spark-defaults.conf.template
- Add the masters url in the file
- spark.master spark://machinename:7077 (it can also start with IP or a bigger name like machinename:7077
- Go to /sbin/spark-env.sh
- Add the following lines to it
- export SPARK_WORKER_MEMORY=1g You can specify how much memory you wanna give to workerexport SPARK_WORKER_INSTANCES=2 → No of workers
export SPARK_MASTER_IP=spark-2 → Name of Spark masterSlave - Go to slave Machine /sbin/start-slave.sh
- Run JPS in both slaves and master
Note : You need a password less access between master and copy masters pub key defined in : id_rsa.pub move to authorized_key in slave and save.
Very Useful links
http://blog.cloudera.com/blog/2015/03/how-to-tune-your-apache-spark-jobs-part-1/
http://blog.cloudera.com/blog/2015/05/working-with-apache-spark-or-how-i-learned-to-stop-worrying-and-love-the-shuffle/
https://www.codementor.io/spark/tutorial/spark-python-rdd-basics